Conjunto de Mandelbrot y Julia
Objetivo:
Demostrar gráficamente los fractales con algoritmo de Benoit Mandelbrot y Gaston Julia
Justificación:
Los números complejos se representan en un plano, de manera que cada número complejo tiene asociado un punto del plano y viceversa. Esta identificación entre puntos y números es lo que nos interesa saber para poder comprender la representación de los fractales que tratamos con Julia y Mandelbrot en sus ecuaciones.
Conjuntos de Julia y Mandelbrot se obtiene a partir de funciones cuadráticas simples, como por ejemplo: Fc(z) = z2 + c , donde c es un número complejo.
Un objeto matemático es un fractal si cumple con las siguientes condiciones:
- Ser lo suficientemente irregular para ser descrito en términos geométricos tradicionales.
- Poseer detalles apreciables a cualquier escala de observación, ser autosimilar (sus partes se parecen al todo).
- Poseer una dimensión de Hausdorff-Besicovitch mayor que su dimensión topológica.
- Poder ser definido mediante un simple algoritmo recursivo.
Origen
Mostrar cuál es la motivación del origen de los conjuntos de Julia y Mandelbrot.
Los sistemas dinámicos tienen su origen al estudiar los problemas de evolución. Con un ejemplo me parece que se va a entender la idea.
Ejemplo: Supongamos que la función f (x)= λx^2 modela la evolución de una población al cabo de un año. Esto es, si tenemos una población inicial de x individuos, al cabo de un año la población será de individuos.
En general nos van a interesar dos problemas: Fijado el parámetro λ , cuál sería la evolución de una población inicial, al cabo de n años; o fijada la población inicial de 0 x individuos, en qué manera afecta el parámetro λ a la evolución de la población.
Ejemplo 2: Siguiendo el ejemplo anterior fijemos λ = 1, entonces resulta que
f x = x^2n .
Este modelo es bastante simple y sencillo, pero no es demasiado realista. Otros modelos más reales, muestran un comportamiento mucho más complicado.
Un ejemplo de esta clase de modelos es la función logística f (x) = λx (1− x) , que en apariencia es apenas un poco más complicada que el ejemplo precedente, pero su comportamiento es bastante más complicado.
El estudio del comportamiento de ésta dio origen al famoso conjunto de Mandelbrot, que veremos más adelante.
Antes de seguir, vamos a definir algunas cosas que nos van a resultar útiles más adelante. Sea f :C → C una función que modela la evolución de un sistema. Dentro del estudio de los sistemas dinámicos nos va a interesar aquellos subconjuntos de C que permanezcan invariantes por la acción de f ; se dicen invariantes en general y los podemos clasificar en:
- Si f (G) = G , entonces G se dice invariante hacia adelante.
- Si f G = G , entonces G se dice invariante hacia atrás.
- Si G cumple ambas propiedades se dice invariante hacia atrás y hacia adelante.
Vista esta pequeña introducción a los sistemas dinámicos, podemos pasar a las teorías especificas de cada modelo.
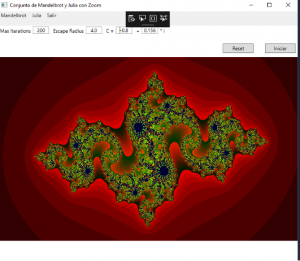
Teoria Julia
El conjunto de Julia que se obtiene a partir de esta función se denota Fc. El proceso para obtener este conjunto de Julia de es el siguiente:
Se elige un número complejo cualquiera z y se va construyendo una sucesión de números de la siguiente manera:
z0 = z
z1 = F(z0)= z02 + c
z2 = F(z1) =z12+c
zn+1 = F(zn) =zn2+c
Si esta sucesión queda acotada, entonces se dice que z pertenece al conjunto de Julia de parámetro c, denotado por Jc; de lo contrario, si la sucesión tiende al infinito, z queda excluido de éste.
Es fácil deducir que obtener un conjunto de Julia resulta muy laborioso, pues el proceso anterior habría que repetirlo para cualquier número complejo z, e ir decidiendo en cada caso si dicho número pertenece o no al conjunto Jc.
El conjunto de Julia tiene ciertas propiedades:
- Es no vacío.
- Es un conjunto invariante hacia adelante y hacia atrás.
- Es acotado y cerrado.
- Tiene interior vacío y no tiene puntos aislados (se dice perfecto).
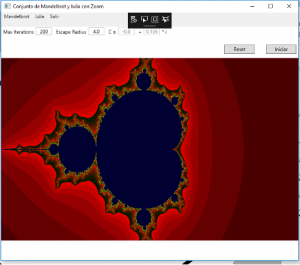
Teoria de Mandelbrot
El conjunto de Mandelbrot es el conjunto de números complejos c para los cuales la sucesión de puntos obtenida por el método iterativo
z0 =0
z1 = F(z0)= z02 + c
z2 = F(z1) =z12+c
……………………….
zn+1 = F(zn) =zn2+c
no tiende a infinito, es decir, está acotada.
El conjunto de Mandelbrot tiene propiedades diferentes de conjuntos de Julia se reparten en diferentes regiones del conjunto M.
- fc tiene un punto fijo atractivo si y solo si c pertenece al interior de la cardioide de ecuación z=1/2eiq(1−1/2eiq, 0<q≤2p. Además, los conjuntos de Julia asociados a estos parámetros son curvas cerradas simples.
- fc tiene un dos-ciclo atractivo si y solo si |c+1|<1/4, esto es, si c está en el mayor de principal. Además, los conjuntos de Julia asociados a estos parámetros son uniones de una cantidad numerable de curvas cerradas simples disjuntas 3 a 3. Estas curvas están formadas por las componentes conexas que contienen a los dos puntos del 2-ciclo atractivo y por todas sus preimágenes.
- En los dos círculos siguientes en tamaño se encuentran los parámetros asociados a conjuntos de Julia para los que la dinámica presenta un ciclo de orden 3 atractivo y cuyos conjuntos de Julia son uniones de una cantidad numerable de curvas cerradas simples disjuntas 4 a 4 y con la propiedad de que donde se tocan 2 se toca también una tercera. Estas curvas están formadas por las componentes conexas que contienen a los tres puntos del 3-ciclo atractivo y por todas sus preimágenes. Los puntos de contacto son todas las preimágenes de uno de los puntos fijos de fc.
Código Fuente VB.Net con wpf
Codigo visual en WPF:
<Window x:Class=”MainWindow”
xmlns=”http://schemas.microsoft.com/winfx/2006/xaml/presentation”
xmlns:x=”http://schemas.microsoft.com/winfx/2006/xaml”
xmlns:d=”http://schemas.microsoft.com/expression/blend/2008″
xmlns:mc=”http://schemas.openxmlformats.org/markup-compatibility/2006″
xmlns:local=”clr-namespace:uno”
mc:Ignorable=”d”
Title=”Conjunto de Mandelbrot y Julia con Zoom” Height=”650″ Width=”750″>
<StackPanel>
<DockPanel Name=”Main” LastChildFill=”False”>
<Menu Height=”35″ Name=”Menu” DockPanel.Dock=”Top”>
<MenuItem Header=”Mandelbrot” Name=”mnmandelbrot” />
<MenuItem Header=”Julia” Name=”mnjulia” />
<MenuItem Header=”Salir” Name=”mnsalir” />
</Menu>
</DockPanel>
<StackPanel Orientation=”Horizontal”
Margin=”5,2,5,2″>
<TextBlock Margin=”0,2,0,0″>Max
Iterations</TextBlock>
<TextBox Name=”tbIterations” Text=”50″
TextAlignment=”Center” Width=”40″
Margin=”5,0,10,5″/>
<TextBlock Margin=”0,2,0,0″>Escape
Radius</TextBlock>
<TextBox Name=”tbRadius” Text=”2″
TextAlignment=”Center” Width=”40″
Margin=”5,0,10,5″/>
<TextBlock Margin=”0,2,0,0″>C =</TextBlock>
<TextBox Name=”tbCReal” Text=”1.1″
TextAlignment=”Center” Width=”40″
Margin=”5,0,10,5″/>
<TextBlock Margin=”0,2,0,0″>+</TextBlock>
<TextBox Name=”tbCImag” Text=”0″
TextAlignment=”Center” Width=”40″
Margin=”5,0,5,5″/>
<TextBlock Margin=”0,2,0,0″>* i</TextBlock>
</StackPanel>
<StackPanel Orientation=”Horizontal”
Margin=”5,5,5,10″ HorizontalAlignment=”Right”>
<Button Content=”Reset” Height=”23″ HorizontalAlignment=”Center” Margin=”28,12,0,0″ Name=”button1″ VerticalAlignment=”Top” Width=”75″ Click=”button1_Click” />
<Button Content=”Iniciar” Name=”button2″ Width=”75″ Height=”23″ Margin=”28,12,0,0″/>
</StackPanel>
<Grid>
<Canvas Name=”Canvas1″ MouseLeftButtonDown=”Canvas1_MouseLeftButtonDown” MouseLeftButtonUp=”Canvas1_MouseLeftButtonUp” MouseMove=”Canvas1_MouseMove”>
<Image Name=”image1″ Height=”450″ Width=”750″ />
<TextBlock Name=”textointro” FontSize=”15″ HorizontalAlignment=”Center” VerticalAlignment=”Center” TextAlignment=”Center” Width=”750″>
Bienvenido <LineBreak/>
<LineBreak/>
Selecciona el fractal que desas visualizar en el menu superior <LineBreak/>
<LineBreak/>
Angel Grajales Perez M:207201617
</TextBlock>
</Canvas>
</Grid>
</StackPanel>
</Window>
Código en VB.net
Imports System.Numerics
Class MainWindow
Inherits Window
Dim bandera As Integer
Private NIterations As Integer
Private MaxRadius2 As Double
Private Cx0 As Double
Private Cy0 As Double
Private area As Rect = New Rect(New Point(-2.0, -1.0), New Point(2.0, 1.0))
Private selection As Rectangle = New Rectangle() With {
.Stroke = Brushes.Blue,
.StrokeThickness = 1,
.Visibility = Visibility.Collapsed
}
Private mousedown1 As Boolean = False
Private mousedownpos As Point
Public Sub New()
InitializeComponent()
Initializar()
End Sub
Private Sub Initializar()
tbCReal.Text = “-0.8”
tbCImag.Text = “0.156”
tbIterations.Text = “200”
tbRadius.Text = “4.0”
MaxRadius2 = 4.0
Cx0 = -0.8
Cy0 = 0.156
NIterations = 200
Canvas1.Children.Add(selection)
End Sub
‘boton de reset para ambos casos
Private Sub button1_Click(ByVal sender As Object, ByVal e As RoutedEventArgs)
If (bandera = 1) Then
area = New Rect(New Point(-2.0, -1.0), New Point(2.0, 1.0))
image1.Source = drawSet(area)
ElseIf (bandera = 2) Then
area = New Rect(New Point(-2.0, -1.0), New Point(2.0, 1.0))
image1.Source = drawSet2(area)
End If
End Sub
‘funcion que grafica mandelbrot
Private Function drawSet(ByVal area As Rect) As WriteableBitmap
NIterations = Int32.Parse(tbIterations.Text)
MaxRadius2 = 2.0 * Double.Parse(tbRadius.Text)
Dim PixelHeight As Integer = CInt(Math.Truncate(image1.Height))
Dim PixelWidth As Integer = CInt(Math.Truncate(image1.Width))
Dim wbmap As WriteableBitmap = New WriteableBitmap(PixelWidth, PixelHeight, 96, 96, PixelFormats.Pbgra32, Nothing)
Dim BytesPerPixel As Integer = wbmap.Format.BitsPerPixel \ 8
Dim pixels As Byte() = New Byte(PixelHeight * PixelWidth * BytesPerPixel – 1) {}
Dim s As Integer = PixelWidth * BytesPerPixel
Dim xscale As Double = (area.Right – area.Left) / PixelWidth
Dim yscale As Double = (area.Top – area.Bottom) / PixelHeight
Dim i As Integer = 0
While i < pixels.Length
Dim py As Integer = i \ s
Dim px As Integer = (i Mod s) \ BytesPerPixel
Dim x As Double = area.Left + px * xscale
Dim y As Double = area.Top – py * yscale
Dim z As Complex = New Complex(x, y)
Dim count As Integer = mandelbrot(z)
Dim C1 As Color = colorMap(count)
pixels(i) = C1.B
pixels(i + 1) = C1.G
pixels(i + 2) = C1.R
pixels(i + 3) = C1.A
i += BytesPerPixel
End While
wbmap.WritePixels(New Int32Rect(0, 0, PixelWidth, PixelHeight), pixels, s, 0)
Return wbmap
End Function
‘funcion que grafica julia
Private Function drawSet2(ByVal area As Rect) As WriteableBitmap
NIterations = Int32.Parse(tbIterations.Text)
MaxRadius2 = 2.0 * Double.Parse(tbRadius.Text)
Dim PixelHeight As Integer = CInt(Math.Truncate(image1.Height))
Dim PixelWidth As Integer = CInt(Math.Truncate(image1.Width))
Dim wbmap As WriteableBitmap = New WriteableBitmap(PixelWidth, PixelHeight, 96, 96, PixelFormats.Pbgra32, Nothing)
Dim BytesPerPixel As Integer = wbmap.Format.BitsPerPixel \ 8
Dim pixels As Byte() = New Byte(PixelHeight * PixelWidth * BytesPerPixel – 1) {}
Dim s As Integer = PixelWidth * BytesPerPixel
Dim xscale As Double = (area.Right – area.Left) / PixelWidth
Dim yscale As Double = (area.Top – area.Bottom) / PixelHeight
Dim i As Integer = 0
While i < pixels.Length
Dim py As Integer = i \ s
Dim px As Integer = (i Mod s) \ BytesPerPixel
Dim x As Double = area.Left + px * xscale
Dim y As Double = area.Top – py * yscale
Cx0 = Double.Parse(tbCReal.Text)
Cy0 = Double.Parse(tbCImag.Text)
Dim c As Complex = New Complex(Cx0, Cy0)
Dim z As Complex = New Complex(x, y)
Dim count As Integer = julia(c, z)
Dim C1 As Color = colorMap(count)
pixels(i) = C1.B
pixels(i + 1) = C1.G
pixels(i + 2) = C1.R
pixels(i + 3) = C1.A
i += BytesPerPixel
End While
wbmap.WritePixels(New Int32Rect(0, 0, PixelWidth, PixelHeight), pixels, s, 0)
Return wbmap
End Function
‘ color de 4 bits con rgb y alpha para los colores
Private Function colorMap(ByVal count As Integer) As Color
Dim C As Color = New Color()
C.B = CByte((count \ 100) * 25)
count = count Mod 100
C.G = CByte((count \ 10) * 25)
C.R = CByte((count Mod 10) * 25)
C.A = 255
Return C
End Function
‘algortimo de mandelbrot
Private Function mandelbrot(ByVal c As Complex) As Int32
Dim count As Int32 = 0
Dim z As Complex = Complex.Zero
While count < NIterations AndAlso z.Magnitude < MaxRadius2
z = z * z + c
count += 1
End While
Return count
End Function
‘ algortimo de julia
Private Function julia(ByVal c As Complex, ByVal z As Complex) As Int32
Dim count As Int32 = 0
While count < NIterations AndAlso z.Magnitude < MaxRadius2
z = z * z + c
count += 1
End While
Return count
End Function
‘ zoom cuando se presiona el boton
Private Sub Canvas1_MouseLeftButtonDown(ByVal sender As Object, ByVal e As MouseButtonEventArgs)
mousedown1 = True
mousedownpos = e.GetPosition(Canvas1)
Canvas.SetLeft(selection, mousedownpos.X)
Canvas.SetTop(selection, mousedownpos.Y)
selection.Width = 0
selection.Height = 0
selection.Visibility = Visibility.Visible
End Sub
‘zoom cuando se suelta el boton
Private Sub Canvas1_MouseLeftButtonUp(ByVal sender As Object, ByVal e As MouseButtonEventArgs)
selection.Visibility = Visibility.Collapsed
Dim xscale As Double = (area.Right – area.Left) / image1.Width
Dim yscale As Double = (area.Top – area.Bottom) / image1.Height
Dim TopLeft As Point = New Point(area.Left + Canvas.GetLeft(selection) * xscale, area.Top – Canvas.GetTop(selection) * yscale)
Dim BottomRight As Point = TopLeft + New Vector(selection.Width * xscale, -selection.Height * yscale)
area = New Rect(TopLeft, BottomRight)
If (bandera = 1) Then
image1.Source = drawSet(area)
ElseIf (bandera = 2) Then
image1.Source = drawSet2(area)
End If
End Sub
Private Sub Canvas1_MouseMove(ByVal sender As Object, ByVal e As MouseEventArgs)
If mousedown1 Then
Dim mousepos As Point = e.GetPosition(Canvas1)
Dim diff As Vector = mousepos – mousedownpos
Dim TopLeft As Point = mousedownpos
If diff.X < 0 Then
TopLeft.X = mousepos.X
diff.X = -diff.X
End If
If diff.Y < 0 Then
TopLeft.Y = mousepos.Y
diff.Y = -diff.Y
End If
selection.Width = diff.X
selection.Height = diff.Y
Canvas.SetLeft(selection, TopLeft.X)
Canvas.SetTop(selection, TopLeft.Y)
End If
End Sub
Private Sub Mnmandelbrot_Click(sender As Object, e As RoutedEventArgs) Handles mnmandelbrot.Click
‘guarda bandera el valor para identificar que conjunto mostrara
bandera = 1
tbCReal.IsEnabled = “False”
tbCImag.IsEnabled = “False”
textointro.Visibility = Visibility.Hidden
‘dibuja el conjunto y su area
area = New Rect(New Point(-2.0, -1.0), New Point(2.0, 1.0))
image1.Source = drawSet(area)
End Sub
Private Sub Mnsalir_Click(sender As Object, e As RoutedEventArgs) Handles mnsalir.Click
‘Metodo para salir
System.Windows.Application.Current.Shutdown()
End Sub
Private Sub Mnjulia_Click(sender As Object, e As RoutedEventArgs) Handles mnjulia.Click
‘guarda bandera el valor para identificar que conjunto mostrara
bandera = 2
tbCReal.IsEnabled = “True”
tbCImag.IsEnabled = “True”
textointro.Visibility = Visibility.Hidden
‘dibuja el conjunto y su area
area = New Rect(New Point(-2.0, -1.0), New Point(2.0, 1.0))
image1.Source = drawSet2(area)
End Sub
Private Sub Button2_Click(sender As Object, e As RoutedEventArgs) Handles button2.Click
If (bandera = 1) Then
image1.Source = drawSet(area)
ElseIf (bandera = 2) Then
image1.Source = drawSet2(area)
End If
End Sub
End Class
Capturas de pantalla