En matemáticas, un sistema de ecuaciones paramétricas permite representar una curva o
superficie en el plano o en el espacio, mediante valores que recorren un intervalo de
números reales, mediante una variable, llamada parámetro, considerando cada
coordenada de un punto como una función dependiente del parámetro.
En el uso estándar del sistema de coordenadas, una o dos variables (dependiendo de si se
utilizan dos o tres dimensiones respectivamente) son consideradas como variables
independientes, mientras que la restante es la variable dependiente, con el valor de esta
siendo equivalente al de la imagen de la función cuando los restantes valores son sus
parámetros.
Esta representación tiene la limitación de requerir que la curva sea una función. No todas
las curvas cumplen con dicha condición. Para poder trabajar con la misma como si se
tratara de una función, lo que se hace es elegir un dominio y una imagen diferentes, en
donde la misma sí sea función. Para hacer esto, tanto x como y son considerados
variables dependientes, cuyo resultado surge de una tercera variable (sin representación
gráfica) conocida como «parámetro».
Encontraremos diferentes ecuaciones parametricas las cuales nos generan algunas de la
siguientes figuras:
Epitrocoide, Hipotrocoide, Cicloide, Deltoide, Figuras de Lissajous.
Epitrocoide:
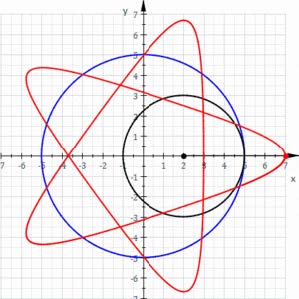
Cicloide:
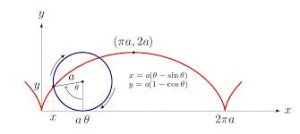
Deltoide:
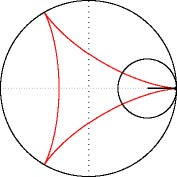
Lissajous:
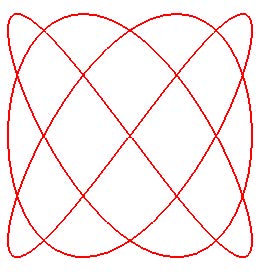
Hipotrocoide:
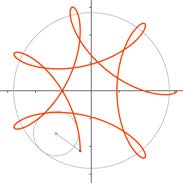
Ahora vamos a generar cada una de las figuras en un programa con VB.
Algoritmo Epitrocoide:
Dim X, Y As Single
X = (RadioCG + RadioCE) * Math.Sin(AnguloCirculo)
Y = (RadioCG + RadioCE) * Math.Cos(AnguloCirculo)
e.Graphics.DrawEllipse(New Pen(Color.BlueViolet, 3), X – RadioCE, Y – RadioCE, 2 *
RadioCE, 2 * RadioCE)
‘Colocamos el lapiz sobre el circulo externo. El lapíz dibujara la curva Epitrocoide
Dim X1, Y1 As Single
X1 = (RadioCG + RadioCE) * Math.Sin(AnguloCirculo) – d * Math.Sin(((RadioCG +
RadioCG + RadioCE) / RadioCE) * AnguloCirculo)
Y1 = (RadioCG + RadioCE) * Math.Cos(AnguloCirculo) – d * Math.Cos(((RadioCG +
RadioCG + RadioCE) / RadioCE) * AnguloCirculo)
e.Graphics.DrawLine(New Pen(Color.Gray, 3), X, Y, X1, Y1)
‘El extremo del lapiz dibuja la curva parametrica epitrocoide
Dim Puntos As Point = New Point(X1, Y1)
TrazoEpitrocoide.Add(Puntos)
For i = 1 To TrazoEpitrocoide.Count – 1
e.Graphics.DrawLine(New Pen(Color.OrangeRed, 4), TrazoEpitrocoide(i),
TrazoEpitrocoide(i – 1))
Next
Algoritmo Cicloide:
Dim X, Y As Single
X = RadioCI * (AnguloCirculo – Math.Sin(AnguloCirculo))
Y = RadioCI * (1 – Math.Cos(AnguloCirculo))
e.Graphics.DrawEllipse(New Pen(Color.BlueViolet, 3), (AnguloCirculo + X) – posIn, (0 –
2 * RadioCI), 2 * RadioCI, 2 * RadioCI)
‘Colocamos el lapiz sobre el circulo. El lapíz dibujara la curva cicloide
Dim X1, Y1 As Single
X1 = RadioCI + RadioCI * (AnguloCirculo – Math.Sin(AnguloCirculo))
Y1 = -RadioCI * (1 – Math.Cos(AnguloCirculo))
e.Graphics.DrawLine(New Pen(Color.Gray, 3), (AnguloCirculo + X + RadioCI) – posIn, (0
– RadioCI), X1 – posIn, Y1)
‘El extremo del lapiz dibuja la curva
Dim Puntos As Point = New Point(X1 – posIn, Y1)
TrazoEpitrocoide.Add(Puntos)
For i = 1 To TrazoEpitrocoide.Count – 1
e.Graphics.DrawLine(New Pen(Color.OrangeRed, 4), TrazoEpitrocoide(i),
TrazoEpitrocoide(i – 1))
Next
Algoritmo Deltoide:
Dim X, Y As Single
X = (RadioCG – RadioCE) * Math.Sin(Angulo_Circulo)
Y = (RadioCG – RadioCE) * Math.Cos(Angulo_Circulo)
e.Graphics.DrawEllipse(New Pen(Color.BlueViolet, 3), X – RadioCE, Y – RadioCE, 2 *
RadioCE, 2 * RadioCE)
‘Colocamos el Lapiz Sobre el Circulo Externo, el lapiz dibujara la curva Deltoide
Dim X1, Y1 As Single
X1 = (RadioCG – RadioCE) * Math.Sin(Angulo_Circulo) + RadioCE *
Math.Sin(Angulo_Circulo * (1 – (RadioCG / RadioCE)))
Y1 = (RadioCG – RadioCE) * Math.Cos(Angulo_Circulo) + RadioCE *
Math.Cos(Angulo_Circulo * (1 – (RadioCG / RadioCE)))
e.Graphics.DrawLine(New Pen(Color.Gray, 3), X, Y, X1, Y1)
‘El Circulo Externo con el Lapiz Dijuba la curva parametrica Deltoide
Dim Puntos As Point = New Point(X1, Y1)
TrazoDeltoide.Add(Puntos)
For i = 1 To TrazoDeltoide.Count – 1
e.Graphics.DrawLine(New Pen(Color.OrangeRed, 4), TrazoHipocicloide(i),
TrazoDeltoide (i – 1))
Next
Algoritmo Hipotrocoide:
Dim X, Y As Single
X = (RadioCG – RadioCI) * Math.Sin(AnguloCirculo)
Y = (RadioCG – RadioCI) * Math.Cos(AnguloCirculo)
e.Graphics.DrawEllipse(New Pen(Color.BlueViolet, 3), X – RadioCI, Y – RadioCI, 2 *
RadioCI, 2 * RadioCI)
‘Colocamos el lapiz sobre el circulo INTERNO. El lapíz dibujara la curva hipotrocoide
Dim X1, Y1 As Single
X1 = (RadioCG – RadioCI) * Math.Cos(AnguloCirculo) + d * Math.Cos(((RadioCG –
RadioCI) / RadioCI) * AnguloCirculo)
Y1 = (RadioCG – RadioCI) * Math.Sin(AnguloCirculo) – d * Math.Sin(((RadioCG –
RadioCI) / RadioCI) * AnguloCirculo)
e.Graphics.DrawLine(New Pen(Color.Gray, 3), X, Y, X1, Y1)
‘El extremo del lapiz dibuja la curva parametrica Hipotrocoide
Dim Puntos As Point = New Point(X1, Y1)
TrazoHipotrocoide.Add(Puntos)
For i = 1 To TrazoHipotrocoide.Count – 1
e.Graphics.DrawLine(New Pen(Color.OrangeRed, 4), TrazoHipotrocoide(i),
TrazoHipotrocoide(i – 1))
Next